Van der Waals’ Equation for Real Gases

The general gas equation is not applicable to real gases at the all the temperature .and pressure. In order to make it applicable to real gases Van der Waals’ made correction in volume and pressure of the gases and derived an equation known as Van der Waals’ equation.

1. Volume Correction

The actual volume of gas molecules is not negligible as compared to volume of the gas. The observed volume is greater than ideal volume, therefore effective volume should be subtracted from the observed volume for the sake of correction. The effective volume is four times of the actual volume of the gas molecules. It is represented by “b” for one mole of a gas. For ‘n’ moles of gas its value would be nb.

Corrected Volume = V = V_observed – nb                     ———-(i)

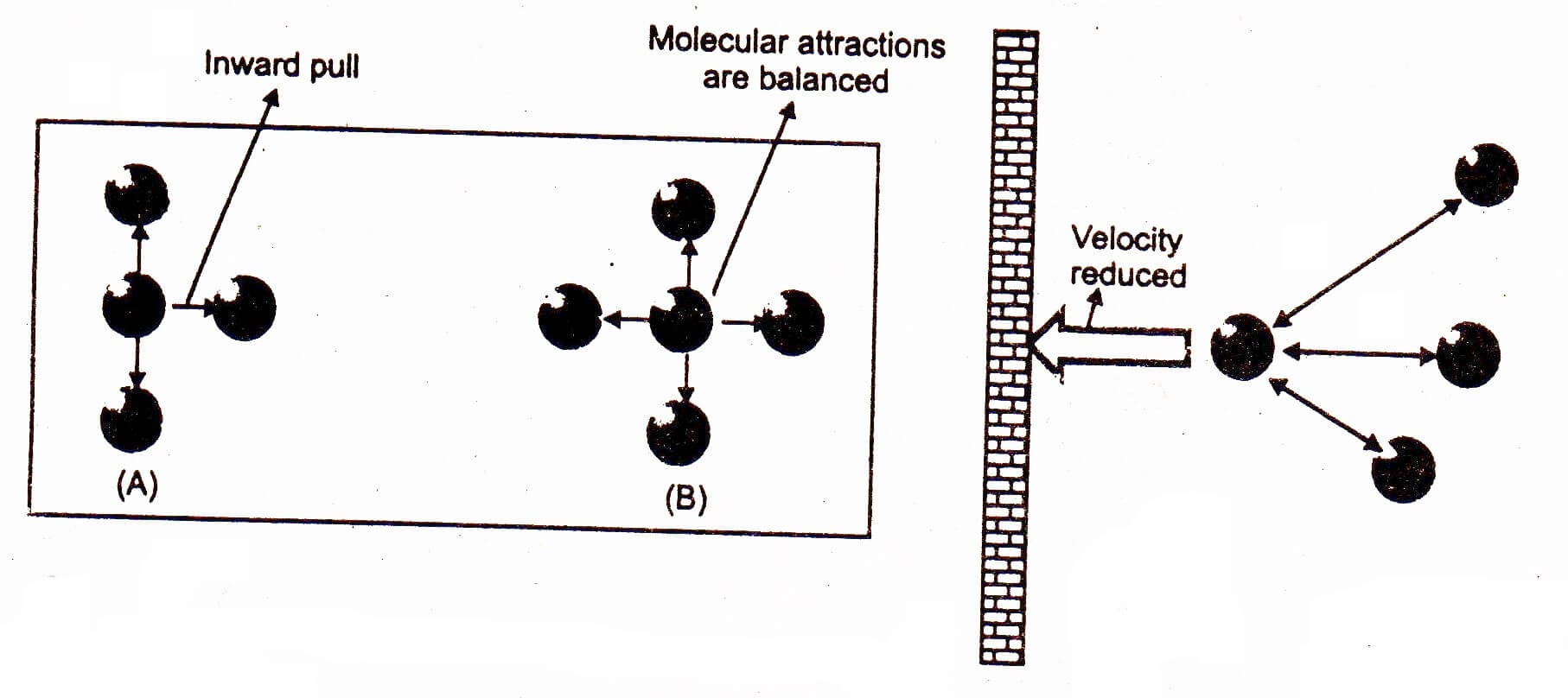
2. Pressure Correction

Pressure of a gas is the result of collisions between the molecules of the gas and walls of the container. Since the colliding molecules are attracted by the other molecules of the gas, therefore their velocity decreases, which causes to reduce the pressure of the gas equal to P’. The pressure P’ should be added to the observed pressure for the sake of correction.

P_i = P+P’               ———-(ii)

Where,   P’ (density)²

P’  n²/v²

Or             P’=a x n₂/v₂     ———– (iii)

Where,   a=Van der Waal’s constant

So, equation (i) becomes,

P_i=P+ an²/v²     ———–(iv)

As we know, the General or Ideal gas equation for gases is,

PV=nRT             ———— (v)

Now, putting values of P & V from equation (i) & equation (iv) in equation (v), we get

(P+an²/v²)(V-nb)=nRT

This is the Van der Waals’ equation.

In this equation ‘a’ and ‘b’ are Van der Waals’ constant.

a is expressed in atm dm⁶ mol^-2 or in Nm⁴ mol^-2,

Whereas,

b is expressed in dm³ mol^-1 or in m³ mol^-1.

When the value of n= 1, then Van der Waal’s equation becomes:

(P+ a/v²)(V – b) = RT

The value of ‘a’ and ‘b’ can be determined by the values of P, V and T of a gaseous system under two different conditions.