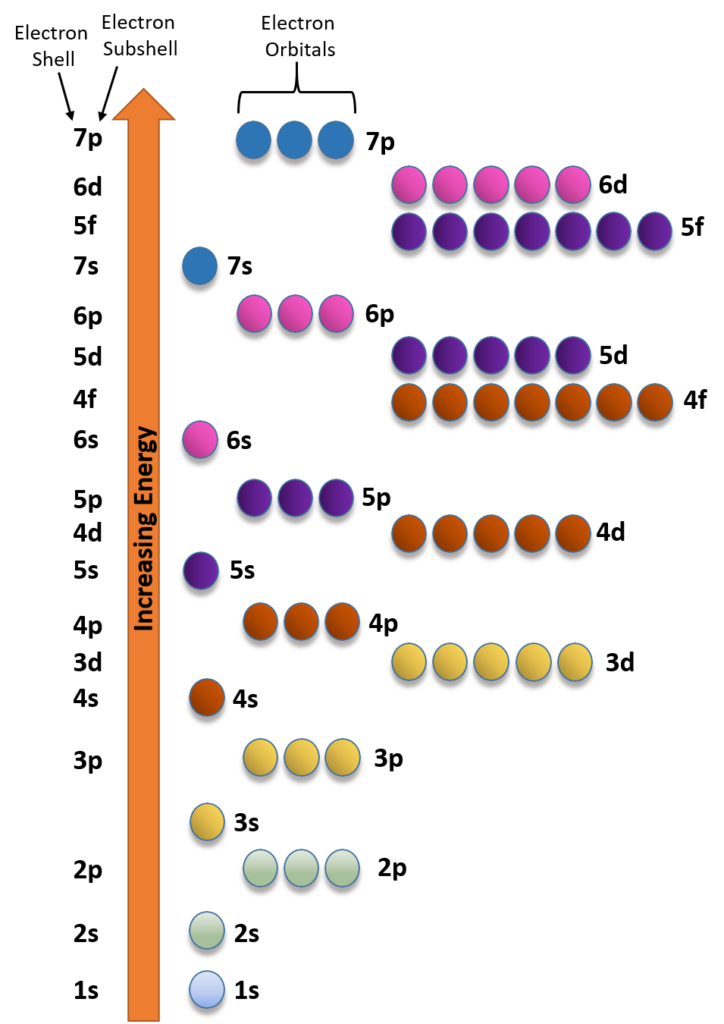
The energies of the hydrogen atom’s orbitals depend only on the principal quantum number [n]; the energy increases as n increases. For this reason, the orbitals belonging to the same level have the same energy regardless of the sublevel they belong to.
Let us compare the emission spectra of the hydrogen atom with that of the helium atom. It can be seen that the latter has more lines than that of hydrogen since, in a helium atom, there are more possible transitions that correspond to emissions in the visible field for a hydrogen atom. This is due to the division of energy levels attributable to the electrostatic interaction between electrons.
Unlike the hydrogen atom, where the energy of an orbital depends only on the value of [n], the energy of a multielectronic system depends both on the value of [n] and on those of [l].
The scheme shows the general order of the energies of the orbitals in multielectronic atoms. Unlike the hydrogen atom, in which the energy of an orbital depends only on the value of [n], the energy of a multielectronic system depends both on the value of [n] and on those of [l].
Pauli Exclusion Principle
Pauli’s exclusion principle states that two electrons in an atom cannot have all quantum numbers equal.
Suppose two electrons of an atom have the same values of [n], [l], and [m], which means they occupy the same orbital. In that case, they must have different values of [m s], i.e., one must have m s = + 1 / 2 and the other m s = -1 / 2.
An atomic orbital can always be at most occupied by two electrons having opposite spins.
We can represent the electron arrangement of an atom by using orbital diagrams in which each orbital is represented with a box with an inscribed symbol. The diagrams for the hydrogen and helium atoms in their fundamental configuration are:
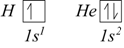
The up arrow indicates one of the two possible spins (one of the two possible values of m s) of the electron. In the case of helium the symbol indicates that there are two 1s electrons with opposite spin.
Principle of the Aufbau
It is possible to write the electronic configuration of all elements based on the energies sequence for the orbitals and the Pauli Exclusion Principle.
This procedure is based on the Aufbau principle, making it possible to construct the periodic table of the elements by determining their electronic configuration progressively.
Each step requires adding an electron to the appropriate orbital.
After helium, the next element in the periodic table is lithium, which has three electrons.
Due to the Pauli Exclusion Principle, an orbital cannot host more than one electron, so the third electron cannot stay in the 1s orbital:
It will have to occupy the next orbital with the lowest possible energy. Therefore, the electron configuration of lithium is 1s2, 2s1.
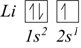
In a similar way, we obtain the electronic configuration of beryllium, which has four electrons as 1s2, 2s2.
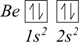
Now both the 1s and 2s orbitals are fully occupied, while the next element, boron, has five electrons and its extra electron must be positioned in the 2p sublevel as all three 2p sublevels have the same energy (they are degenerate ). It can indifferently occupy any of them.
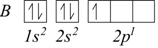
Hund’s Rule
Hund’s rule or principle of maximum multiplicity states that if two electrons occupy degenerate orbitals, with equal values of [n] and [l], they are distributed with parallel spins on the maximum possible number of these.
The most stable arrangement for electrons in orbitals having the same (degenerate) energy is when the number of electrons with the same spin is maximized. Two electrons with the same spin cannot occupy the same orbital; one can maximize the number of electrons with the same spin only by placing electrons in separate orbitals.
For example, for carbon, the electron configuration is 1s2, 2s2, 2p2.
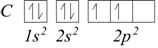
Similarly, for nitrogen we would have 1s2, 2s2, 2p3.
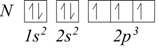
When all the 2p orbitals are singularly occupied, the additional electrons will have to couple with those already present in the orbitals. For oxygen, fluorine and neon we would have:
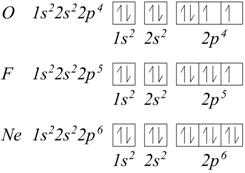
Based on the examples seen, the following general rules can be obtained to derive the electronic configurations of the various atoms:
1) The electrons must occupy the orbitals available at the lowest energy
2) Each orbital can host a maximum of 2 electrons
3) If an empty orbital is available, the electrons do not couple in the same orbital. However, they are distributed in such a way as to occupy all the orbitals available degenerates.
4) The orbitals will fill respecting the pattern of energy levels.
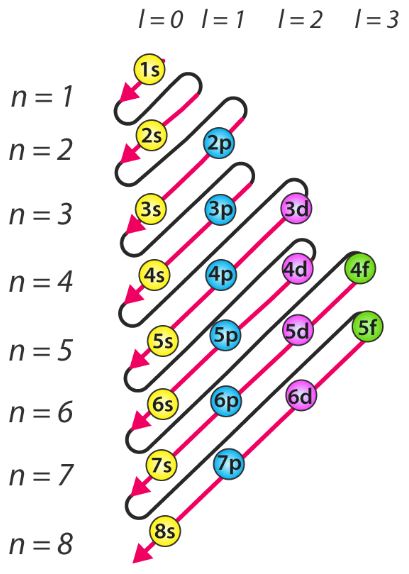
The drawing on the side represents a different scheme to remember the progression of energy levels, taking into account the maximum number of electrons placed on each orbital.
We also recall the conventional rules for indicating the electronic configuration of a chemical element.
Given a chemical element, e.g., Bromine [Br] with atomic number z = 35, the noble gas that precedes the element is sought, in this case, argon [Ar].
The external electrons of the valence configuration are then added. [Br] = [Ar] 4s2, 3d10, 4p5.
Conclusion:
- The hydrogen atom is a relatively simple system, as it contains only one electron.
- The electron can reside in the 1s orbital (ground state) or any other higher energy orbital (excited state).
- With multielectronic systems, there is (at least) the need to know the ground state’s electronic configuration.
- It should also be noted that the relative energies of a multielectronic system’s atomic orbitals are different from those of a monoelectronic system such as the hydrogen atom.



