According to the Planck’s Quantum theory of radiations light shows a dual character, i.e., it behaves both as a material particle and as a wave. This idea was extended to matter particles in 1924 by Louis de-Broglie. According to de-Broglie, all matter particles in motion have a dual character. It means that electrons, protons, neutron, atom and molecules possess the characteristic of both the material particle and a wave. This is called wave-particle duality in thematter.
De Broglie derived a mathematical equation, which relates the wavelength (a) of the electron to the momentum of electron.
Deriving the De Broglie Wavelength
De Broglie derived his equation using well-established theories as follows:
Einstein’s famous equation relating matter and energy:
E=mc2 (1)
Where
E = energy,
m = mass,
c = speed of light
Using Planck’s quantum equation:
E=hv (2)
Where
E = energy,
h = Plank’s constant (6.62607 x 10-34 J s),
v = frequency
Since de Broglie believed particles and wave have the same nature, so, equations 1 & 2 are equal:
mc2=hv (3)
Because real particles do not travel at the speed of light, De Broglie submitted velocity ( v) for the speed of light (c).
mv2=hv (4)
Through the equation λ, de Broglie substituted v/λ, for v and arrived at the final expression that relates wavelength and particle with speed.
mv2=hv/λ (5)
Hence
λ=hv/mv2=h/mv (6)
A majority of Wave-Particle Duality problems is a simple plug and chug via Equation (6) with some variation of cancelling out units. The value of wavelength (λ) of electron while moving in the first orbit of H-atom is comparable to the wavelength of X-rays and can be measured. If we imagine proton moving in a straight line with the same velocity as mentioned for electron, its wavelength would be 1836 times smaller than that of the electron. Similarly, a-particle moving with the same velocity should have a wavelength 7344 times shorter as compared to that of the electron. Now, consider a stone of mass one gram moving with a velocity of 10 m/s, and then its wavelength will be:
6.66×10-34 Js * 10-kgx10 m/s
= 6.65X10-30 m
This wavelength is so smaller that it cannot be measured by any conceivable method. It means that heavy material particles have the waves, but they cannot be captured, and we say that the macroscopic bodies do not have the waves.
Experimental Verification of Dual Nature of Matter
In 1927, two American scientists, Davisson and Germer, experimented with verifying the wave-nature of moving electron. The electrons were produced from heated tungsten filament and accelerated through charged plates.
Davisson and Germer proved that accelerated electrons, lines X-rays, also undergo diffraction when they fall nickel crystal. In this way, the wave nature of the electron was verified.
Heisenberg’s Uncertainty Principle
According to Bohr’s theory, an electron is a material particle and its position, as well as momentum, can be determined with great accuracy. However, with the advent of the concept of the wave nature of the electron, it has not been possible for us to measure the exact position and velocity of the electron simultaneously. Heisenberg suggested this in 1927.
Principle:
If one knows the precise momentum of the particle, it is impossible to know the precise position and vice versa. Heisenberg defined uncertainties in the products of “conjugate pairs” (momentum/position) as having a minimum value corresponding to Planck’s constant divided by 4π. More clearly:
ΔpΔx≥h4π
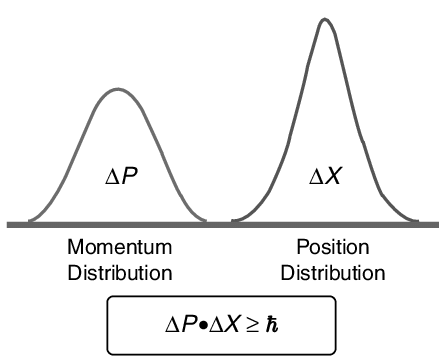
Where Δ refers to the uncertainty in that variable and h is Planck’s constant.
This relationship is called uncertainty principle. This equation shows that if Δx is small then Δp will be large and vice versa.
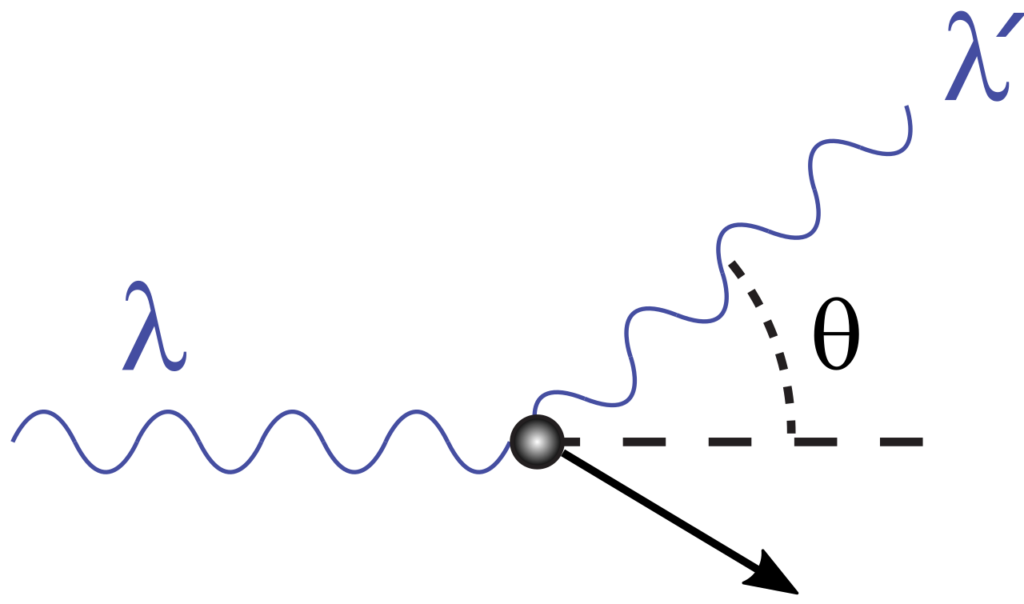
Compton’s Effect
Compton’s effect can help us to understand the uncertainty principle. Suppose we wish to determine the position of an electron. Visible light cannot help us because the wavelength of visible light is millions time large as compared to the diameter of an electron. For this purpose, we have to use X-rays, which have a very short wavelength as compared to that of visible light. When this photon of X-rays strikes an electron, the momentum of an electron will change. In other words, the uncertainty of momentum will appear due to the change of velocity of the electron. Smaller the wavelength of X-rays, greater will be the energy of the photon. Hence, the collision of X-rays with electron will bring about the greater uncertainty in momentum. When we use the photons of longer wavelength to avoid the change of momentum, the determination of the position of the electron becomes impossible.